This is more complicated!
It is derived from the section in Plato's Timeaus which
follows on directly after his description of the Lamda
(Timeaus, 6) which describes the "composition of the soul".
Next, he (God) filled in the double and treble intervals by cutting off further sections and inserting them in the gaps, so there were two mean terms in each interval,
one exceeding one extreme and being exceeded by the other by the same fraction of the extremes; the other exceeding and being exceeded by the same numerical amount.
These links produced intervals of 3/4 and 4/3 and 9/8 within the previous intervals, and he went on to fill all the intervals of 4/3 with the interval 9/8; this left, as a remainder in each, an interval whose terms bore the numerical ratio of 256 to 243. And at that stage the mixture from which these sections were being cut was all used up".
The first part of the clause in italics refers to the Harmonic Mean, the second to the Arithmetic Mean. In other words the Harmonic Mean is the mean exceeding one extreme, and being exceeded by the other, by the same fraction of the extremes.
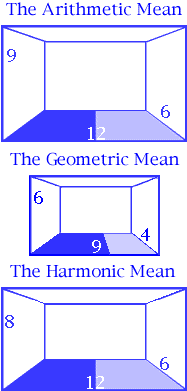
Palladio uses the example of a room six feet wide by twelve feet long which has a ceiling height of eight feet. The mean, 8, exceeds the smaller extreme, 6, by a third of the smaller extreme; 2, just as it (the mean) is itself exceeded by the same fraction (a third) of the larger extreme, 12, which is 4.
This is expressed as: (8-6) divided by 6 = (12-8) divided by 12,
or, where b is the mean between the two extremes a and c:
(b-a) divided by a = (c-b) divided by c.
Practically, this is found by multiplying the greater and lesser extremes and dividing the result by the Arithmetical Mean found in the first example.
Thus 12 times 6 gives 72, which is then divided by the arithmetical mean, 9, to give the answer 8 which is the harmonic mean; the height of the room.
Another way of doing this, if you don't want to find the Arithmetic Mean first, is to multiply the greater by the lesser, 12 x 6 = 72, then multiply that result by two, 2 x 72 = 144, and then divide that result by the sum of the two extremes (6 and 12):
Thus; 144 divided by (6 + 12), that is, 144 divided by 18 = 8.
This can be remembered by the following formula;
b = 2ac divided by (a+c).
Here is a summary of all three Means:

And a summary of all three means as applied to Rooms: